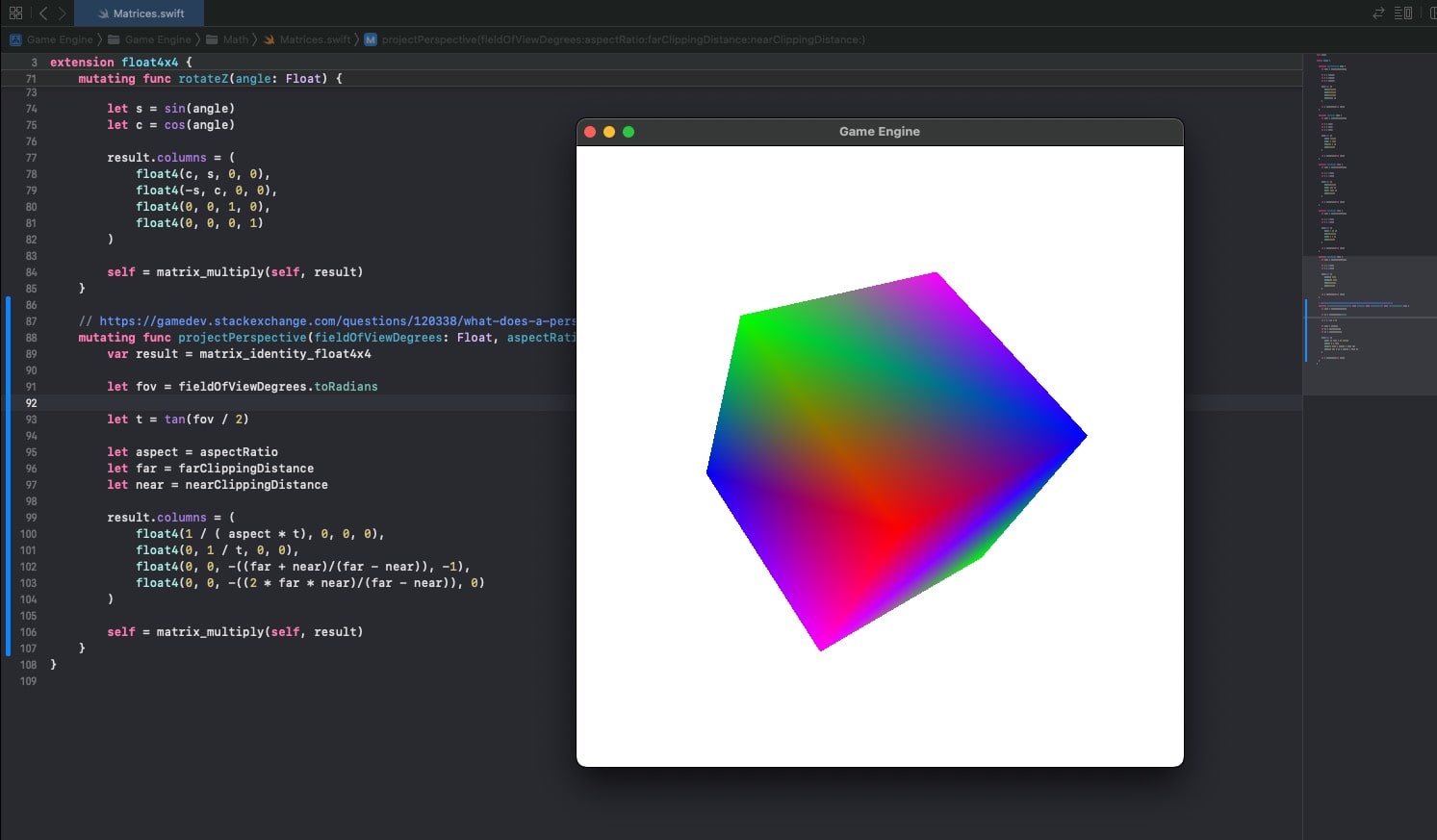
3D Perspective Projection Matrix (Metal Part 11)

z4gon
z4gon

Setting up the the 3D perspective projection matrix to transform view space coordinates in homogeneous clip space coordinates. Later on the GPU takes in these and calculates the Normalized Device Coordinates, to finally calculate the actual Screen Space coordinates. Configuring the Depth Stencil in Metal, to perform Depth Testing and clipping based on depth, using the Depth Texture. Multiplying the projection matrix by the view space coordinates vector during the Vertex Shader Function stage.

Source Code

See Project in GitHub 👩‍💻

References

Table of Content

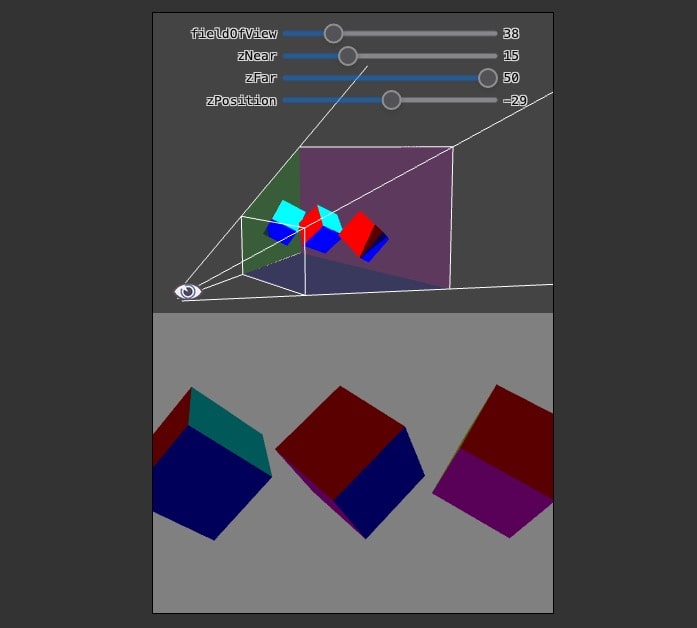
3D Perspective Projection Matrix

View Frustrum

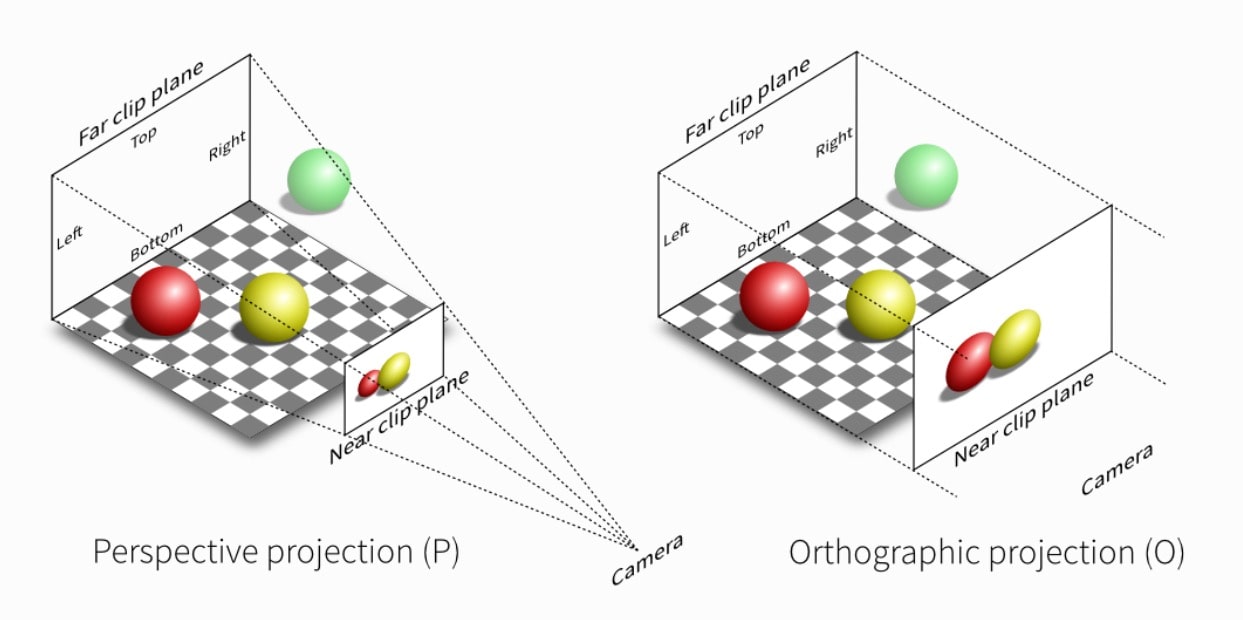
Projecting 3D objects onto a flat surface means connecting each vertex to the position of the camera, and pin pointing where that line crosses the near clip plane.

Picture

Image Source 🔗

Clipping

The near and far clip planes determine what gets rendered in terms of depth.

The field of view means how much stuff gets into the projection in terms of bounds vertically and horizontally.

Picture

Image Source 🔗

Matrix

All the calculations can be put into a pre-determined matrix that can be multiplied by a position vector and it will return the homogenous clip space coordinates.

Metal will then translate these to Normalized Device Coordinates ranging from (-1, -1) to (1, 1) and including depth.

Finally this will be translated to screen space as x, y coordinates in pixels.

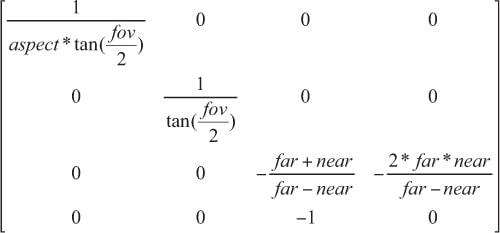
Picture

Image Source 🔗

This is what it looks like in code:

1mutating func projectPerspective(fieldOfView: Float, aspectRatio: Float, farClippingDistance: Float, nearClippingDistance: Float) {
2    var result = matrix_identity_float4x4
3
4    let fov = fieldOfView
5    let aspect = aspectRatio
6    let far = farClippingDistance
7    let near = nearClippingDistance
8
9    result.columns = (
10        float4(Float(1) / ( aspect * tan(fov / Float(2)) ), 0, 0, 0),
11        float4(0, Float(2) / tan(fov / Float(2)), 0, 0),
12        float4(0, 0, -((far + near)/(far - near)), -1),
13        float4(0, 0, -((2 * far * near)/(far - near)), 0)
14    )
15
16    self = matrix_multiply(self, result)
17}

Cube Mesh

To define a cube mesh, we need just 8 vertices.

And then an array of indexes to define all the counter clockwise triangles that will make up the quad faces.

1class CubeMesh : Mesh{
2    override func createMesh() {
3        vertices = [
4            Vertex(position: float3( 0.5, 0.5, 0.5), color: float4(1,0,0,1)), // FRONT Top Right
5            Vertex(position: float3(-0.5, 0.5, 0.5), color: float4(0,1,0,1)), // FRONT Top Left
6            Vertex(position: float3(-0.5,-0.5, 0.5), color: float4(0,0,1,1)), // FRONT Bottom Left
7            Vertex(position: float3( 0.5,-0.5, 0.5), color: float4(1,0,1,1)),  // FRONT Bottom Right
8
9            Vertex(position: float3( 0.5, 0.5, -0.5), color: float4(0,0,1,1)), // BACK Top Right
10            Vertex(position: float3(-0.5, 0.5, -0.5), color: float4(1,0,1,1)), // BACK Top Left
11            Vertex(position: float3(-0.5,-0.5, -0.5), color: float4(1,0,0,1)), // BACK Bottom Left
12            Vertex(position: float3( 0.5,-0.5, -0.5), color: float4(0,1,0,1))  // BACK Bottom Right
13        ]
14
15        // counter clockwise mean out facing
16        indices = [
17
18            // FRONT face
19            0,1,2,
20            0,2,3,
21
22            // BACK face
23            5,4,7,
24            5,7,6,
25
26            // TOP face
27            4,5,1,
28            4,1,0,
29
30            // BOTTOM face
31            6,7,3,
32            6,3,2,
33
34            // LEFT face
35            1,5,6,
36            1,6,2,
37
38            // RIGHT face
39            4,0,3,
40            4,3,7
41        ]
42    }
43}

Depth Stencil

Descriptor

To let the GPU know what vertices are farther away from the camera, and then be able to clip them using the Depth Test, we need to setup the Depth Stencil Descriptor.

State

We will use the descriptor to create the Depth Stencil State, and pass it on to the Render Command Encoder.

1public struct LessDepthStencilState: DepthStencilState {
2    var name: String = "Less DepthTest"
3    var depthStencilState: MTLDepthStencilState!
4
5    init(){
6
7        let depthStencilDescriptor = MTLDepthStencilDescriptor()
8        depthStencilDescriptor.depthCompareFunction = MTLCompareFunction.less
9        depthStencilDescriptor.isDepthWriteEnabled = true
10
11        depthStencilState = Engine.device.makeDepthStencilState(descriptor: depthStencilDescriptor)
12    }
13}

Pixel Format

The Render Pipeline Descriptor and the MTKView will both need to set the Depth Stencil Pixel Format as well, just like they set the Color Pixel Format.

1public struct BasicRenderPipelineDescriptor: RenderPipelineDescriptor{
2    ...
3
4    init(){
5
6        ...
7
8        // make the pixel format match the device
9        renderPipelineDescriptor.colorAttachments[0].pixelFormat = Preferences.PixelFormat
10        renderPipelineDescriptor.depthAttachmentPixelFormat = Preferences.DepthStencilPixelFormat
11
12        ...
13    }
14}
1class GameView: MTKView {
2
3    var renderer: GameViewRenderer!
4
5    required init(coder: NSCoder) {
6        super.init(coder: coder)
7
8        device = MTLCreateSystemDefaultDevice()
9        clearColor = Preferences.ClearColor
10        colorPixelFormat = Preferences.PixelFormat
11        depthStencilPixelFormat = Preferences.DepthStencilPixelFormat
12
13        Engine.initialize(device: device!)
14
15        renderer = GameViewRenderer(self)
16        delegate = renderer
17    }
18}

Mesh Renderer

The mesh renderer will pass the Depth Stencil State to the Render Command Encoder.

1func doRender(renderCommandEncoder: MTLRenderCommandEncoder) {
2    ...
3    renderCommandEncoder.setDepthStencilState(DepthStencilStateCache.getDepthStencilState(.Less))
4    ...
5}

Camera

The camera will use its properties to calculate the Perspective Projection Matrix.

1class Camera : Component, EarlyUpdatable {
2
3    public var viewMatrix: float4x4 = matrix_identity_float4x4
4    public var projectionMatrix: float4x4 = matrix_identity_float4x4
5
6    public var type: CameraType = CameraType.Perspective
7
8    public var fieldOfView: Float = 60
9    public var nearClippingDistance: Float = 0.1
10    public var farClippingDistance: Float = 1000
11
12    ...
13
14    func updateProjectionMatrix() {
15        var result: float4x4 = matrix_identity_float4x4
16
17        if(type == CameraType.Perspective) {
18            result.projectPerspective(
19                fieldOfViewDegrees: fieldOfView,
20                aspectRatio: GameViewRenderer.AspectRatio,
21                farClippingDistance: farClippingDistance,
22                nearClippingDistance: nearClippingDistance
23            )
24        }
25
26        projectionMatrix = result
27    }
28
29    // to ensure all other components get the accurate camera position
30    func doEarlyUpdate(deltaTime: Float) {
31        updateViewMatrix()
32        updateProjectionMatrix()
33    }
34}

Scene

The Scene will include the projection matrix in its Scene Constants that will get passed down to the GPU.

1class Scene : Transform {
2
3    private var _sceneConstants: SceneConstants! = SceneConstants()
4
5    ...
6
7    func updateSceneConstants() {
8        _sceneConstants.viewMatrix = CameraManager.mainCamera.viewMatrix
9        _sceneConstants.projectionMatrix = CameraManager.mainCamera.projectionMatrix
10    }
11
12    override func render(renderCommandEncoder: MTLRenderCommandEncoder) {
13
14        updateSceneConstants()
15
16        // set the view matrix
17        renderCommandEncoder.setVertexBytes(&_sceneConstants, length: SceneConstants.stride, index: 2)
18
19        super.render(renderCommandEncoder: renderCommandEncoder)
20    }
21}

Shader

In the Shader code, we will use the projection matrix to multiply it by the rest of the matrices and the position, to complete the transformation of the coordinates into homogenous clip space.

1float4 HCPosition = ProjMatrix * ViewMatrix * ModelMatrix * objectPosition;
1struct SceneConstants {
2    float4x4 viewMatrix;
3    float4x4 projectionMatrix;
4};
5
6vertex FragmentData basic_vertex_shader(
7  // metal can infer the data because we are describing it using the vertex descriptor
8  const VertexData IN [[ stage_in ]],
9  constant ModelConstants &modelConstants [[ buffer(1) ]],
10  constant SceneConstants &sceneConstants [[ buffer(2) ]]
11){
12    FragmentData OUT;
13
14    // return the vertex position in homogeneous screen space
15    // ProjectionMatrix * ViewMatrix * ModelMatrix * ObjectPosition = HSCPosition
16    OUT.position = sceneConstants.projectionMatrix
17                    * sceneConstants.viewMatrix
18                    * modelConstants.modelMatrix
19                    * float4(IN.position, 1);
20
21    OUT.color = IN.color;
22
23    return OUT;
24}

Result

Now the cube appears projected correctly in the screen space plane.

Picture